viernes, 23 de agosto de 2013

Agentes autómatas

  
 Introducción 

En esta investigación conoceremos más acerca de agentes autómatas, compuertas lógicas  leyes de Morgan, mapas de Kargnaugh , como simular un circuito en worbench y memorias biestables. 

Agentes Autómatas
Introducción
La teoría de autómatas es el estudio de dispositivos de cálculo abstractos, es decir, de las “máquinas”. Antes de que existieran las computadoras, en la década de los años treinta, A. Turing estudió una máquina abstracta que tenía todas las capacidades de las computadoras de hoy día, al menos en lo que respecta a lo que podían calcular. El objetivo de Turing era describir de forma precisa los límites entre lo que una máquina de cálculo podía y no podía hacer; estas conclusiones no sólo se aplican a las máquinas abstractas de Turing, sino a todas las máquinas reales actuales.
En las décadas de los años cuarenta y cincuenta, una serie de investigadores estudiaron las máquinas más simples, las cuales todavía hoy denominamos “autómatas finitos”. Originalmente, estos autómatas se propusieron para modelar el funcionamiento del cerebro y, posteriormente, resultaron extremadamente útiles para muchos otros propósitos.

 Autómata finito
Se define en términos de sus estados, la entrada que acepta y su reacción ante la misma. Hay autómatas finitos de 2 tipos: Deterministas y no Deterministas, dependiendo de cómo se defina la capacidad para cambiar el estado.

Funcionamiento de los autómatas finitos Deterministicos (AFD).
Consiste en ir pasando de un estado a otro, a medida que va recibiendo los caracteres de la palabra de entrada. Simplemente hay que pasar de estado a estado siguiendo las flechas de transiciones para cada carácter de la palabra de entrada, empezando por el estado inicial. Este proceso puede llevarse a cobo en los diagramas de estado y el camino recorrido se visualiza como una trayectoria.


Autómata Finito Determinista (AFD)
Es una quíntupla D = (Q; Σ; δ;s; F ) donde:
Q es un conjunto finito de estados.
Σ es un alfabeto de finito.
δ es una función de transición, finita.
s es el estado inicial.
F es una colección de estados finales o de aceptación.

Autómata Finitos No Deterministicos (AFND)

Hay dos formas posibles de entender como funciona un AFND.
La primera es pensar que cuando hay varias alternativas, el AFND elige una de ellas. Si existe una forma de elegir el siguiente estado que me lleve finalmente a aceptar la cadena, entonces el AFND  la aceptaría.
La segunda forma es imaginarse que el AFND esta en varios estados a la vez ( en todos en los que "puede estar" de acuerdo a la primera visión). Si luego leer la cadena puede estar en un estado final, acepta la cadena. En cualquier caso, es bueno por un rato no pensar en como implementar un AFND.

Una libertad adicional que permitiremos en los AFNDs es la de rotular las transiciones
con cadenas, no sólo con caracteres. Tal transición se puede seguir cuando los caracteres de
la entrada calzan con la cadena que rotula la transición, consumiendo los caracteres de la
entrada. Un caso particularmente relevante es el de las llamadas transiciones-ε, rotuladas
por la cadena vacía. Una transición-ε de un estado p a uno q permite activar q siempre que
se active p, sin necesidad de leer ningún carácter de la entrada.

Autómata Finito Determinista (AFND)
Es una quíntupla D = (Q; Σ; δ;s; F ) donde:
Q es un conjunto finito de estados.
Σ es un alfabeto de finito.
δ es una función de transición, finita.
s es el estado inicial.
F es una colección de estados finales o de aceptación.



Compuertas Lógicas
Las compuertas lógicas son dispositivos que operan con aquellos estados lógicos mencionados en la página anterior y funcionan igual que una calculadora, de un lado ingresas los datos, ésta realiza una operación, y finalmente, te muestra el resultado.


 
Cada una de las compuertas lógicas se las representa mediante un Símbolo, y la operación que realiza (Operación lógica) se corresponde con una tabla, llamada Tabla de Verdad.
 Compuerta NOT
Se trata de un inversor, es decir, invierte el dato de entrada, por ejemplo; si pones su entrada a 1 (nivel alto) obtendrás en su salida un 0 (o nivel bajo), y viceversa. Esta compuerta dispone de una sola entrada. Su operación lógica es s igual a  a invertida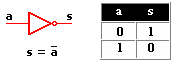


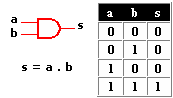
Compuerta AND
Una compuerta AND tiene dos entradas como mínimo y su operación lógica es un producto entre ambas, no es un producto aritmético, aunque en este caso coincidan.

*Observa que su salida será alta si sus dos entradas están a nivel alto*


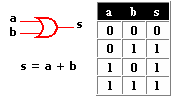
Compuerta OR
Al igual que la anterior posee dos entradas como mínimo y la operación lógica, será una suma entre ambas... Bueno, todo va bien hasta que 1 + 1 = 1, el tema es que se trata de una compuerta O Inclusiva es como a y/o b.

*Es decir, basta que una de ellas sea 1 para que su salida sea también 1*


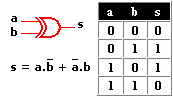
 Compuerta OR-EX o XOR
Es OR EXclusiva en este caso con dos entradas (puede tener mas entradas) y lo que hará con ellas será una suma lógica entre a por b invertida y a invertida por b.

*Al ser O Exclusiva su salida será 1 si una y sólo una de sus entradas es 1*

Leyes de Morgan
Son una parte de la Lógica proposicional, analítica ,y fueron creada por Augustus de Morgan; estas declaran las reglas de equivalencia en las que se muestran que dos proposiciones pueden ser lógicamente equivalentes.

Las Leyes de Morgan permiten:

El cambio del operador de conjunción en operador de disyunción y viceversa.  Las proposiciones conjuntivas o disyuntivas a las que se aplican las leyes de Morgan pueden estar afirmadas o negadas (en todo o en sus partes).
Casos:

¬(P ^ Q) ≡ (¬P v ¬Q)

Si nos encontramos con una proposición conjuntiva totalmente negada, la ley de Morgan nos permite transformarla en una proposición disyuntiva con cada uno de su miembros negados

¬(P v Q) ≡ (¬P ^ ¬Q)

Si nos encontramos con una proposición disyuntiva totalmente negada, la ley de Morgan nos permite transformarla en una proposición conjuntiva con cada uno de sus miembros negados

(P ^ Q) ≡ ¬ (¬ P v ¬ Q)

Si nos encontramos con una proposición conjuntiva afirmada, la ley de Morgan nos permite transformarla en una proposición disyuntiva negada en su totalidad y en sus miembros.

(P v Q) ≡ ¬(¬P ^ ¬Q)

Si nos encontramos con una proposición disyuntiva afirmada, la ley de Morgan nos permite transformarla en una proposición conjuntiva negada en su totalidad y en sus miembros.


 Mapas de Kargnaugh
Un mapa de Kargnaugh se conoce  como tabla de Kargnaugh o  diagrama de Veitch(abreviado mapa-K o mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas; este mapa fue inventado en 1950 por Maurice Kargnaugh.
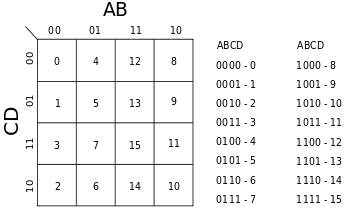
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Kargnaugh tendrá 16 celdas, distribuidas en una cuadricula de 4 × 4.

La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 10 porque el resultado de la función es ƒ = 10 cuando A = 1, B = 0, C = 1, D = 0. Una vez construido el mapa de Kargnaugh, la siguiente tarea es la de seleccionar conjunto de términos denominados subcubos de manera que se obtenga el menor número de subcubos posible. Estos subcubos se seleccionan formando grupos de rectángulos que encierren a los unos del mapa, las áreas deben ser potencia de 2 (ej. 1, 2, 4, 8, ...) y se debe tratar de agrupar el mayor número de unos posible. En resumen hay que tomar en cuenta al hacer estos grupos de unos (subcubos) lo siguiente:

  • Debemos utilizar todos los unos del mapa.
  • Es mejor crear el menor numero de grupos.
  • Los unos pueden estar en varios grupos.
  • El número de unos dentro de un grupo debe de ser cualquier potencia de 2.
  • Mientras más grande sea un grupo la simplificación de la función será mejor.
  • No es necesario que todos los grupos tengan el mismo tamaño.


Construcción del mapa-K.
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Kargnaugh tendrá 16 celdas.
Como simular un circuito en Workbench

Memorias Biestables.
Un biestable, también llamado báscula (flip-flop en inglés), es un multivibrador capaz de permanecer en un estado determinado o en el contrario durante un tiempo indefinido. Esta característica es ampliamente utilizada en electronica digital para memorizar información. El paso de un estado a otro se realiza variando sus entradas. Dependiendo del tipo de dichas entradas los biestables se dividen en asíncronos y síncronos.
La principal diferencia es que el asíncrono solo tiene entradas de control, sin embargo el síncrono dispone además de una entrada para sincronismo o reloj. Si las entradas de control dependen de la de sincronismo se denominan síncronas y en caso contrario asíncronas. Por lo general, las entradas de control asíncronas prevalecen sobre las síncronas.  La entrada de sincronismo puede ser activada por nivel (alto o bajo) o por flanco (de subida o de bajada). Dentro de los biestables síncronos activados por nivel están los tipos RS yD, y dentro de los activos por flancos los tipos JK,T y D.
Un biestable puede usarse para almacenar un bit. La información contenida en muchos biestables puede representar el estado de un secuenciador, el valor de un contador, un carácter ASCII en la memoria de un ordenador, o cualquier otra clase de información. Un uso corriente es el diseño de maquinas de estado finitas electrónicas. Los biestables almacenan el estado previo de la máquina que se usa para calcular el siguiente.
El T es útil para contar. Una señal repetitiva en la entrada de reloj hace que el biestable cambie de estado por cada transición alto-bajo si su entrada T está a nivel 1. La salida de un biestable puede conectarse a la entrada de reloj de la siguiente y así sucesivamente. La salida final del conjunto considerado como una cadena de salidas de todos los biestables es el conteo en codigo binario del número de ciclos en la primera entrada de reloj hasta un máximo de 2n-1, donde n es el número de biestables usados. Una cadena de biestables T como la descrita anteriormente también sirve para la división de la frecuencia de entrada entre 2n, donde n es el número de biestables entre la entrada y la última salida.


Conclusión


El mapa

El mapa de Kargnaugh,  podría considerarse como una especie de tabla de la verdad. Su gran utilidad radica en la posibilidad de minimizar expresiones booleanas.
Las compuertas lógicas son dispositivos electrónicos muy sencillos, pero al mismo tiempo son muy utilizados en el área de la automatización industrial. 

             Bibliografía
 


Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)